授课教师：门博   职称：副教授    所在学院：数学与系统科学学院

一、课程简介

“复变函数论”是数学与应用数学专业的核心课程，是数学分析的后续课程，面向大二本科生开设。本课程的主要内容是讨论单复变量的复值可微函数的性质，其主要研究对象是解析函数。复变函数论作为一种强有力的工具，被广泛应用于自然科学的众多领域。

二、课程思政资源挖掘分析

复变函数的理论与方法经历了近千年的发展，课程内容整体侧重逻辑，偏重推理，要经过给出定义、陈述定理、证明定理、应用方法解题等几个必备的授课环节。在这些教学活动中，适当的引入思政元素会提高学生的学习兴趣，增强学生的学习效果。

本课程把学生的价值观培养放在重要位置，从专业知识、数学历史文化、复变函数论应用前沿信息中适度挖掘思想政治教育资源。转变课程观，增加复变函数论在各领域应用的内容，把握融入的思政内容比例、时机频次、方法技巧，把“价值体系、知识体系、能力体系”有机融合，帮助学生理解马克思主义哲学的基本观点及其运用方法；增强学生的创新意识，培养学生以改革创新为核心的时代精神；培养学生对数学与应用数学专业的情怀，增强新时代大学生勇于创新和挑战的意识。

三、课程思政融入点设计

1. 在线平台分享专业故事，赋予抽象理论以生动的背景，提高学生的学习兴趣，引领学生形成正确的人生观、世界观。

在介绍复变函数发展历程过程中，讲述有重大贡献的华罗庚先生在多复变函数论、典型群方面的研究领先西方数学界十多年，激励学生不断探索、自强不息、刻苦钻研的学习精神，激发学生爱国情怀，增强民族自豪感，引领学生形成正确的人生观和价值观。

在教学过程中，介绍有关定理涉及的其他科学家的事迹。例如法国数学家古萨在函数论、 伪超椭圆积分和微分方程方面的贡献影响了法国数学学派，他对柯西著作的详细分析， 最后得出了著名的柯西-古尔萨定理；挪威数学家阿贝尔少年成才以及在代数和椭圆函数方面的贡献， 而且研究了无穷级数， 得到一些判别准则以及关于幂级数求和的定理。 通过数学家事迹的讲述，不仅使学生了解古今中外数学家及其数学成就，而且可以激励学生不断探索、自强不息、不畏艰难的科学精神。

2. 增加复变函数论应用案例，呈现抽象理论实践场景，增强学生的创新意识，培养学生以改革创新为核心的时代精神。

通过介绍复积分的物理意义，培养学生学以致用的能力；利用参数求不同积分后，引导学生思考积分与积分路径有（无）关的条件，为讲授后续知识做铺垫，提高学生正确认识问题、分析问题和解决问题的能力，培养学生的自主学习，主动探索的精神；利用参数方程法计算复积分，其中 为以为圆心，为半径的正向圆周，为整数， 引导学生关注积分曲线与圆心、半径有关，探究积分值与这两因素的关联，追求严谨的科学精神；利用高科技医疗中核磁共振成像扫描（MBI）技术让医生得以发现处于破裂边缘的动脉瘤，或者精确地找到骨头上出现的微小裂缝，让学生感受小波变换、傅里叶变换在信号处理中的发挥的神奇作用，增强学生的求知欲望和创新意识，培养学生以改革创新为核心的时代精神。

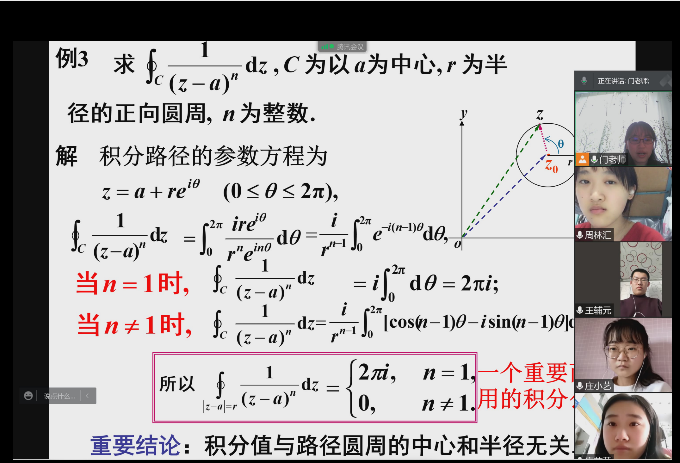
3. 强化复变函数知识中的辩证方法，在线分组讨论，增强学生的思政意识，促进学生理解唯物辩证法的规律和思想方法。

通过论述复变初等函数与实变初等函数的区别：复指数函数 是周期函数，而实指数函数是单调函数； 复变对数函数是多值函数，其中 即可，而实变对数函数是单值函数，且要求 ；乘幂 是正实数；在复数域内，正弦函数与余弦函数不再是有界函数；在复数范围比在实数范围多两个根等等，引导学生以发展的眼光看待事物的发展，才能拥有完整系统的知识体系，进一步揭示事物的矛盾与和谐的统一。通过级数部分和极限的存在性来定义级数的收敛性以及有限项的和到无限项和性质变化，揭示辩证唯物主义中量变到质变的规律。

【2022.3.27发稿】